Big O is a notation used for describing the complexity(whether space or time complexity) of a program. This concept describes how much time it takes to run your function with respect to the size of the input to the function. In this lesson, we will focus on the time complexity of programs.
FACTORS THAT DETERMINE SPEED OF A FUNCTION
How fast is the computer
Running background apps
Type of language used to program
WHAT IS TIME COMPLEXITY?
Time complexity is the amount of time a program takes to or complete its operation. It is a way to show how the runtime of function increases as the size of the input increases. We have different types of time complexity with respect to the size of input which include: Constant, Logarithmic, Linear, Log Linear, Quadratic, Cubic, Exponential, Factorial Time, etc.
Constant Time: This type of notation is known as O(1)[reads as Big O of 1], it is used to describe programs that run in constant time no matter the complexity or size of the input. i.e no matter how large the input from the user is the result remains in constant time. In this case we can say the time taken doesn't increase at all as the size of the input increases.
Logarithmic Time: In this type of notation which is known as O(log n)[read as Big O of log n], the program executes by dividing the size of the input while carrying out the operation on the input. This notation is seen in programs like binary search trees in which each iteration, the function divides the input to optimize the speed of the program. This is sometimes considered the best and faster implementation after O(1) for programs.
Linear Time: Just as the name implies, the size of the input is directly proportional to the time taken to execute the program. As the size of the input increases, the time taken also increases as well. This denotes the time-taken to run a program which is linear just like in the graph (straight-line graph).
Log Linear Time: O(n log n)[read as Big O of n log n] is a notation that implements two different types of complexity i.e O(n) and O(log n)if multiplied. This can notation can be seen in the merge sort algorithm.
Quadratic Time: As the name implies, the graph of this notation is a quadratic graph. "Quadratic" is a Latin word "quadrus" which means square (O(n^2)[read as Big O of n square]). The chart is a parabola, we ignore the negative as we are only interested in the positive aspect.
Cubic Time: Cubic time complexity is triple of the Linear Time complexity (O(n^3)[read as Big O of n cube]). The graph is a cubic graph for showing the time complexity of a function.
Exponential Time: As the size of the input doubles after each operation, the time complexity is said to be exponential (O(2^n)[read as Big O of 2 power n])
Factorial Time: O(n!)[read as Big O of n factorial], in this type of complexity the program grows in a factorial way based on the size of the input. An example can be seen in the Heap Algorithm.
GRAPH OF TIME COMPLEXITY
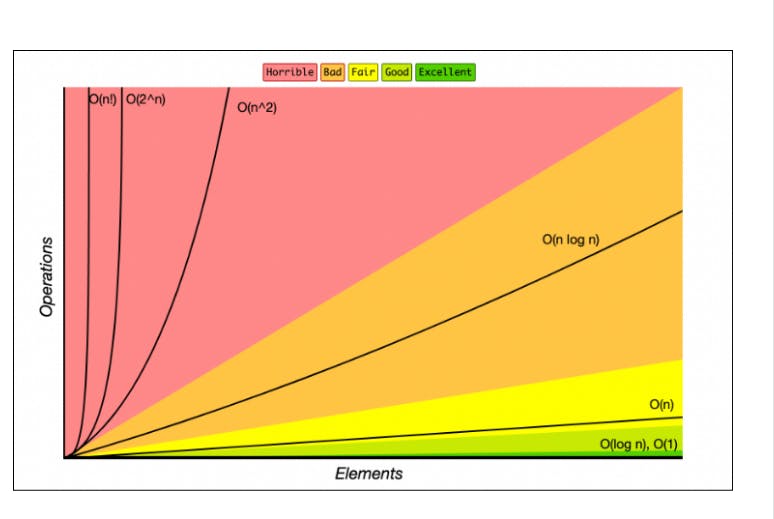
From this graph, we can see which algorithm we could consider the best based no matter the size of the input and the speed of the program.
| O | COMPLEXITY | TIME FRAME |
| O(1) | constant | fast |
| O(log n) | logarithmic | |
| O(n) | linear | |
| O(n * log n) | log linear | |
| O(n ^ 2) | quadratic | |
| O(n ^ 3) | cubic | |
| O(2 ^ n) | exponential | |
| O(n!) | factorial | slow |
It is my greatest desire that growing programmers will have an insight on some of the available time complexity we have and also choose the best that will work we for their programs. Good programs are more efficient and even faster no matter the size of the input.
For more reading, you can consider some of the articles I read that enlighten me on the subject of time complexity.
